Why were wavetables developed?
We now hold early wavetable synths such as the PPGs in high esteem and think of them as expensive examples of early digital synthesisers. However, wavetables were actually invented to make possible relatively low-cost instruments that avoided the shortcomings of existing digital synthesis methods such as FM and additive synthesis, and to overcome the immense technological limitations of the day.
To understand this, imagine that you want to use a piece of audio equipment today to record, store and replay the sound of a someone saying “wow”. You choose a suitable recorder or sampler, capture the sound and, without any need to understand how the equipment does what it does, you can then replay it. If you used a digital recorder, you do so simply by pressing the Play button; if you used a sampler, you allocate the sample to a key or pad, then press that to listen to the recording that you’ve made.
However, we don’t have to travel back many years to a time when none of this was practical. The problem was two-fold. Firstly, early memory chips were extremely limited in capacity, and storing anything more than a fraction of a second of audio was very expensive. Secondly, even if you could store the audio, the primitive microprocessors available at the dawn of digital synthesis were barely able to address the memory and replay it at an adequate speed.
Let’s consider the word “wow”, which takes about a second to say. Using the sampling specification introduced for the audio CD (44,100 16-bit samples per channel per second) you would require 88.2KB of RAM to record the word in mono, and double that if it were recorded in stereo. Nowadays, we wouldn’t blink at that sort of requirement, but when the earliest digital audio equipment appeared, you needed as many as eight chips for just 2KB of RAM. Sure, samplers were shipped with boards stuffed full of dozens of these, but you would have needed no fewer than 352 of them to store the word “wow” at CD quality!
Clearly, this was impractical so, while various digital tape formats were able to provide the hundreds of megabytes of audio data storage needed to edit and master whole albums of music, developers of digital musical instruments were looking at much more efficient ways to record, store and replay sounds for use in synthesis. The wavetable was one such method.
Synths that make you go “wow!”
So… it’s 1979 and you want your keyboard to say “wow”. It’s not impossible – a mere £20,000 (around £100,000 at today’s values) would buy you a Fairlight CMI, which is just about capable of doing this. But instead of emptying your piggy-bank, let’s imagine that you can slice the word into eight pieces, one beginning at the start of the sound, the next 1/8 of a second after the start, the next 1/4 of a second after the start… and so on until it has run its course. If each of these slices was a full eighth of a second (0.125s) long, you could reassemble the entire waveform simply by replaying them in the correct order. But each slice would still require about 10KB of storage, and this will have saved you nothing. But now imagine making each snippet much shorter… say, 0.0125s (of the order of the length of a single cycle of audio when spoken by a human) and separating each by the appropriate length of silence. Each slice would now require about 1KB of RAM and, instead of being a sample in the conventional sense, would represent the sound at a discrete moment as the word was spoken. This is not as daft as it sounds. Tests had showed that – depending on how much data you removed – you could analyse the harmonic content at various moments and then, on replay, use a mathematical method called ‘interpolation’ to fill the gaps between slices with an estimate of the sound that had previously existed. This allowed you to obtain a close approximation to the original sample, but with a much reduced data storage requirement.
With around 8KB of memory required, recreating the word “wow” was getting closer to being practical, but additional space saving measures were still necessary. For example, 16-bit data was a luxury in the early 1980s, so samples were often recorded at a resolution of 8 bits per word, which decreased the memory requirement to just 4KB. Indeed, early digital audio systems often used quite severe compression techniques to reduce the storage still further… in this example, down to around 2KB.
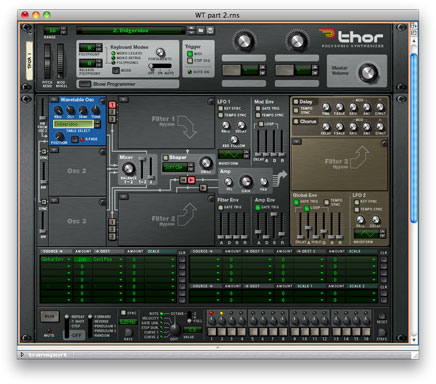
While you don’t need to store all of the audio data to be able to reconstruct a recognisable approximation to the original sound, it becomes increasing difficult as you discard more and more of it. Nonetheless, if you have eight single sample snippets derived in this way, you can reconstruct something that is recognisable. You want proof…? No problem. Let’s turn to the Wavetable Osc in Thor and select the Voice wavetable, as shown in figure 1. If you start with its Position parameter set to zero, and then sweep through the position manually to record the points at which the timbre changes, you’ll find that the wavetable comprises seven waveforms, as shown in table 1.

| Position Value | Waveform generated |
| 0 – 19 | Wave 1 |
| 20 – 39 | Wave 2 |
| 40 – 58 | Wave 3 |
| 59 – 78 | Wave 4 |
| 79 – 97 | Wave 5 |
| 98 – 117 | Wave 6 |
| 118 – 127 | Wave 7 |
If you now sweep through these using the Filter Env contour generator to control the Position as shown in figure 2, you’ll hear that the waves have a slightly vocal quality, although none of them actually sounds like a vocal sample:
(Click to enlarge)
However, I have a bit of inside knowledge, and I know the nature of the sample from which the waves in this wavetable were derived. Armed with this knowledge, I can reassemble it. First, I have to switch the X-Fade button ON. (X-Fade is a very simple example of the mathematical interpolation that I mentioned above, and it will generate a rough estimate of the audio that existed in the gaps between the snippets in the wavetable.) Second, as show in figure 3, I need to set up a different set of envelope parameters to sweep through the waves at the correct rate. Having done so, I can now play a note. Wow indeed:
(Click to enlarge)
Of course, this method of storing and reconstructing sounds is not constrained to the word “wow”, and Thor contains three tables designed to be used in this way: Voice, Piano and Didgeridoo. Figure 4 shows a patch that makes great use of the Didgeridoo wavetable. The thing to note here is that I couldn’t use the Filter Env or Amp Env to sweep through the table because the sound I want to create requires a loop. Furthermore, an LFO wouldn’t be ideal because the two directions of the sweep need to be of unequal rate. But a looping contour generator, on which you can independently determine the length of the A and D stages, is perfect. Sound #3 demonstrates this patch, and there’s no doubting what the original sound was before it was cut up into tiny pieces:
(Click to enlarge)
A different way to use a wavetable
Instead of creating a table that’s designed to play successive snippets of a single sample, imagine one that’s created using snippets from samples recorded at different pitches. For example, you could ask a brass player to play a succession of different notes and then extract the waveform that lies exactly two seconds into each. In theory, you could then allocate these to zones on the keyboard so that the timbral variations of the instrument are correctly mapped from the lowest to the highest notes played. This is the basis of “multi-sampling”, the technique used to create sample libraries and the ROMs within PCM-based digital synthesisers.
Thor contains two wavetables designed for use in this fashion: the Trombone Multi and the Sax Multi. In tutorial #11, I used (or perhaps abused) one of these – the Trombone Multi – to create a sound whose harmonic content varied in time, so let’s now hear how this sounds when the waves are distributed across the keyboard as they were meant to be.
(Click to enlarge)
Figure 5 shows a single Wavetable Osc with its Position parameter set to 40. Below this, you can see three identical paths in the modulation matrix. These cause the Position to change rapidly with respect to MIDI note number, condensing the range of notes over which the waves are distributed so that I can demonstrate them effectively.
Sound #4 was played using this patch, and you can clearly hear the zones in which each wave lies:
These discontinuities would be a nightmare if you were creating the ROM for a digital synthesiser, but in a wavetable synthesiser the differences between groups of notes can be used creatively. To illustrate this, I’ve further developed the patch above to include two Trombone Multis and one Sax Multi, as shown in figure 6. Cheating a little by passing the output from this through Reason’s UN-16 Unison processor and adding a touch of reverb, I obtained sound #5. Hmm… that sounds like something I know and love:
(Click to enlarge)
Of course, there’s nothing stopping you from using a wavetable designed to be played sequentially (such as the Voice wavetable) and distributing it across the keyboard, just as last month I took the Trombone Multi (designed to be distributed across the keyboard) and played it sequentially. Figure 7 shows a wavetable patch with the Voice table inserted, and Position tracking that creates bands in which the various waves play. You can hear this in sound #6:
(Click to enlarge)
To turn this into a useful vocal sound, I’m going to add some gentle vibrato using LFO1, and a slight pitch instability from LFO2. As shown in figure 8, both of these are routed via the modulation matrix to the pitch of Osc1, and you can hear the result in sound #7:
Clearly, each of the four notes has a markedly different timbre, so all I need do is add some chorus and reverb to obtain a wonderful patch that exhibits different vocal characters from one end of the keyboard to the other. All this and, as always, there’s not a single filter in sight:
(Click to enlarge)
Inevitably, life at the dawn of digital synthesis wasn’t quite as simple as these examples imply, and there were many problems to be overcome before it was possible to build a general-purpose wavetable synthesiser. Most notably, it was discovered that the sample snippets usually have to be resynthesised and phase-aligned so that you can loop single samples and cross-fade between adjacent ones. But, while awkward, these problems were not insurmountable and, when the first wavetable synthesisers appeared, their lesser demands for processing power and memory meant that they were very much cheaper than the samplers of the era. But while the PPG Wave 2.2 and Wave 2.3 are now revered by many players, I reckon that they would kill to be able to create the sounds in this tutorial. So don’t underestimate what Thor’s Wavetable Osc can do for you. The world of wavetable synthesis is not limited to delicate chimes, glassy pads and 1980s synth-pop, as some might have you believe.
So many sounds, so little time…
We have now covered the two fundamental aspects of wavetable synthesis: making the sound evolve in time, and changing the timbre at different points across the keyboard. But there’s no reason to stop there, and many fascinating sounds can be derived from using both techniques simultaneously. Unfortunately, I’ll have to leave you to discover them for yourselves, because we’ve come to the end of my tutorials explaining Thor’s oscillators. I hope that they have given you some ideas, and illustrated why there is so much more to synthesis than tweaking the cut-off knobs of resonant low-pass filters. Indeed, I hope that they have illustrated why you don’t need filters at all to be able to create a huge range of fabulous sounds. If so, my job is done. Thank you for reading; I appreciate it.
Text & Music by Gordon Reid